y=xの断面が正三角形となる体積
◆第問目!
曲線\(\displaystyle\hspace{2pt}y = x^2-x\hspace{2pt}\)上に点\(\hspace{1pt}P\hspace{1pt}\)をとり、点\(\hspace{1pt}P\hspace{1pt}\)と直線\(\hspace{2pt}y= x\hspace{2pt}\)の距離を『点と直線の距離の公式』から計算すれば、断面の正三角形の一辺の長さを求めることができます。
点\(\hspace{1pt}(x_0 , y_0)\hspace{2pt}\)と直線\(\hspace{2pt}ax+by+c=0\hspace{2pt}\)における点と直線の距離は $${\frac{|ax_0 + b y_0 +c|}{\sqrt{a^2+b^2}}}$$ から求められます。
正三角形の一辺の長さから、立体\(\hspace{1pt}B\hspace{2pt}\)の断面積である正三角形の断面積を求めることができます。
下図のように、正三角形の一辺の長さを\(\hspace{1pt}L\hspace{1pt}\)とします。
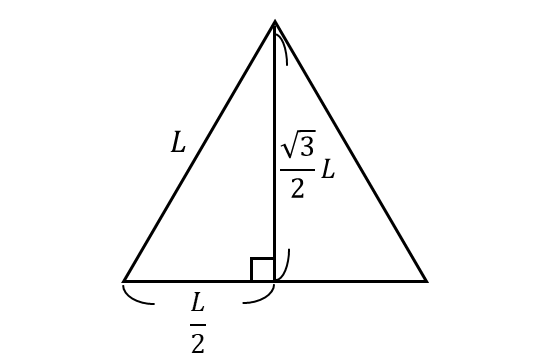
このとき、正三角形の高さは $${\sqrt{L^2 - \left(\frac{L}{2}\right)^2} = \frac{\sqrt{3}}{2}L}$$ であることから、面積\(\hspace{1pt}S\hspace{2pt}\)は $$ \begin{aligned} S & = \frac{1}{2} L \cdot \frac{\sqrt{3}}{2}L \\[1em] & =\frac{\sqrt{3}}{4} L^2 \\ \end{aligned} $$ となります。
求められた正三角形の面積\(\hspace{1pt}S\hspace{1pt}\)を積分して体積\(\hspace{1pt}V\hspace{1pt}\)を求めますが $${V = \int_0^{2} S \hspace{1pt}dx}$$ と計算できない点に注意が必要です。
正三角形は直線\(\hspace{2pt}y= x\hspace{2pt}\)に垂直な平面で切った断面であるため、直線\(\hspace{1pt}y=x\hspace{1pt}\)と平行な方向に軸をとり積分する必要があります。
そこで、以下のように直線\(\hspace{1pt}y=x\hspace{1pt}\)と平行な方向に\(\hspace{1pt}X\hspace{1pt}\)軸を取ります。
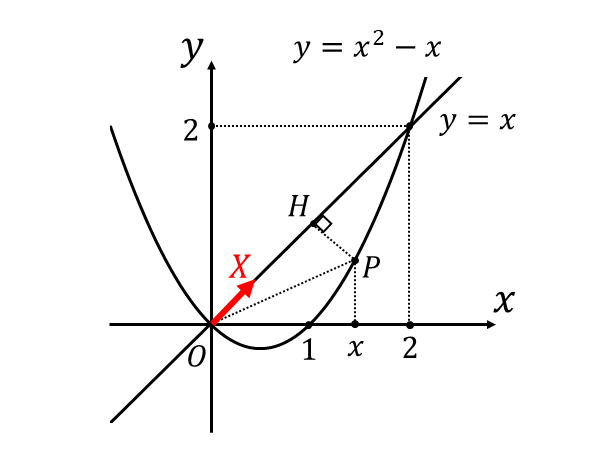
このとき、求める体積\(\hspace{1pt}V\hspace{1pt}\)は $${V = \int_0^{2\sqrt{2}} S \hspace{1pt}dX}$$ となります。
断面積\(\hspace{2pt}S\hspace{2pt}\)を\(\hspace{1pt}x\hspace{1pt}\)の関数で表していれば、上式の\(\hspace{1pt}dX\hspace{1pt}\)を\(\hspace{1pt}dx\hspace{1pt}\)に変換して積分を計算します。
【問題の答え】
\(\displaystyle \frac{2\sqrt{6}}{15} \)
【解答のポイント】
本問は、直線\(\hspace{2pt}y= x\hspace{2pt}\)に垂直な平面で切った断面の正三角形の面積を求め、立体の体積\(\hspace{1pt}V\hspace{1pt}\)を求める問題です。
正三角形の面積\(\hspace{1pt}S\hspace{1pt}\)を積分して体積\(\hspace{1pt}V\hspace{1pt}\)を求めるとき $${V = \int_0^{2} S \hspace{1pt}dx}$$ と計算できない点に注意が必要です。
正三角形は直線\(\hspace{2pt}y= x\hspace{2pt}\)に垂直な平面で切った断面であるため、直線\(\hspace{1pt}y=x\hspace{1pt}\)と平行な方向に軸をとり積分する必要があります。
そこで、以下のように直線\(\hspace{1pt}y=x\hspace{1pt}\)と平行な方向に\(\hspace{1pt}X\hspace{1pt}\)軸を取ることで計算します。

このとき、求める体積\(\hspace{1pt}V\hspace{1pt}\)は $${V = \int_0^{2\sqrt{2}} S \hspace{1pt}dX}$$ となります。
ここで、\(dX\hspace{1pt}\)は\(\hspace{2pt}X\hspace{1pt}\)と\(\hspace{2pt}x\hspace{2pt}\)の関係を求めて微分をすることで求めます。
\(\hspace{2pt}X\hspace{1pt}\)は線分\(\hspace{1pt}OH\hspace{1pt}\)の長さから求められるので、直角三角形\(\hspace{1pt}OPH\hspace{1pt}\)に三平方の定理を用いて
$${\overline{OH}^{\hspace{2pt}2} = \overline{OP}^{\hspace{2pt}2} -\overline{HP}^{\hspace{2pt}2}}$$
から求めます。
【問題の解答】
問題 :『曲線\(\displaystyle\hspace{2pt}y = x^2-x\hspace{2pt}\)と直線\(\hspace{2pt}y= x\hspace{2pt}\)に囲まれる部分を\(\hspace{2pt}A\hspace{2pt}\)とする. \(A\hspace{1pt}\)を底面とし, 直線\(\hspace{2pt}y= x\hspace{2pt}\)に垂直な平面で切った断面が常に正三角形となる立体を\(\hspace{1pt}B\hspace{1pt}\)とする. 立体\(\hspace{1pt}B\hspace{1pt}\)の体積\(\hspace{2pt}V\hspace{2pt}\)を求めよ.』
曲線\(\displaystyle\hspace{2pt}y = x^2-x\hspace{2pt}\)と直線\(\hspace{2pt}y= x\hspace{2pt}\)を図示すると以下のようになります。
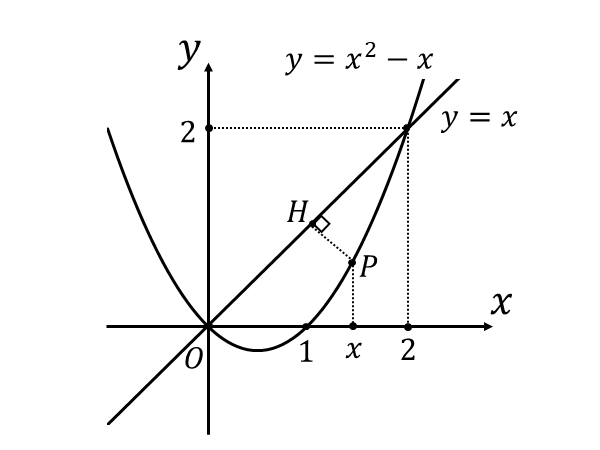
上図において、\(\displaystyle y =x^2 -x\hspace{2pt}\)上に点\(\hspace{1pt}P\)、点\(\hspace{1pt}P\hspace{2pt}\)から直線\(\hspace{2pt}y=x\hspace{2pt}\)に垂直に下した垂線の足を点\(\hspace{1pt}H\hspace{2pt}\)とします。
\(\hspace{1pt}0 \leqq x \leqq 2\hspace{2pt}\)における曲線\(\hspace{2pt}y =x^2 -x\hspace{2pt}\)上の点\(\hspace{1pt}P(x,x^2 -x)\hspace{1pt}\)と直線\(\hspace{2pt}-x+y=0\hspace{1pt}\)の距離\(\hspace{2pt}\overline{HP}\hspace{2pt}\)は点と直線の距離の公式から $$ \begin{aligned} \hspace{10pt} \overline{HP} & = \frac{|-x+(x^2 -x)|}{\sqrt{2}} \\[1em] & =\frac{|x^2-2x|}{\sqrt{2}} \\ & =\frac{-x^2+2x}{\sqrt{2}} \\ \end{aligned} $$ と求められます。
よって、直線\(\hspace{2pt}y=x\hspace{2pt}\)に垂直な平面に立体を切ったときの正三角形の面積\(\hspace{2pt}S\hspace{2pt}\)は $$ \begin{aligned} S & = \frac{\sqrt{3}}{4}(\overline{HP})^2\\[1em] & =\frac{\sqrt{3}}{4} \cdot \frac{\left(-x^2+2x \right)^2}{2} \\ & =\frac{\sqrt{3}}{8}\left(-x^2+2x \right)^2 \\ \end{aligned} $$ となります。
ここで、直線\(\hspace{1pt}y=x\hspace{1pt}\)と平行な方向に\(\hspace{1pt}X\hspace{1pt}\)軸を取ります。

求める体積\(\hspace{1pt}V\hspace{1pt}\)は、断面積\(\hspace{2pt}S\hspace{2pt}\)を\(\hspace{1pt}X\hspace{1pt}\)軸方向に\(\hspace{2pt}0 \leqq X \leqq 2\sqrt{2}\hspace{2pt}\)の区間を積分することで求められるので $${V = \int_0^{2\sqrt{2}} S \hspace{1pt}dX}$$ となります。
ここで、変数\(\hspace{2pt}x\hspace{2pt}\)と\(\hspace{1pt}X\hspace{1pt}\)の関係式を求めます。
\(\hspace{2pt}X\hspace{1pt}\)は線分\(\hspace{1pt}OH\hspace{1pt}\)の長さから求められるので、直角三角形\(\hspace{1pt}OPH\hspace{1pt}\)に三平方の定理を用いると
よって、\(0 \leqq x \leqq 2\hspace{2pt}\)において $${X = \frac{x^2}{\sqrt{2}}}$$ となります。
両辺を\(\hspace{2pt}x\hspace{2pt}\)で微分すると $${\frac{dX}{dx} =\sqrt{2} x}$$ となることから、\(\displaystyle dX = \sqrt{2} x dx\hspace{2pt}\)と表せます。
また、変数\(\hspace{2pt}X\hspace{2pt}\)に対応する変数\(\hspace{2pt}x\hspace{2pt}\)の値は以下のようになります。
| \({X}\) | \({0 \to 2\sqrt{2}}\) |
|---|---|
| \({x}\) | \(\displaystyle{0 \to 2}\) |
以上から
と求められます。
【問題の種類を絞る】