y=tanxの逆関数の定積分の問題と解き方

【答え】
　$\displaystyle \frac{\pi}{4} - \frac{1}{2} \log 2 $
　

【解答のポイント】
　関数$\hspace{2pt}y=\tan x\hspace{2pt}$$\hspace{2pt}(\displaystyle \hspace{1pt} 0 \leqq x \leqq \frac{\pi}{4}\hspace{1pt})\hspace{2pt}$の逆関数を$\hspace{2pt}y=f(x)\hspace{2pt}$とすると $${\int_0^1 y\hspace{1pt}dx}$$ が求める定積分となります。

このとき、$y\hspace{2pt}$は$\hspace{2pt}x\hspace{2pt}$の関数で表すことができないため、$dx\hspace{2pt}$を$\hspace{2pt}dy\hspace{2pt}$に置き換えて積分を計算します。
　

また、本問の定積分は、関数$\hspace{2pt}y=\tan x\hspace{2pt}$とその逆関数$\hspace{2pt}y=f(x)\hspace{2pt}$のグラフの関係性から求めることもできます。

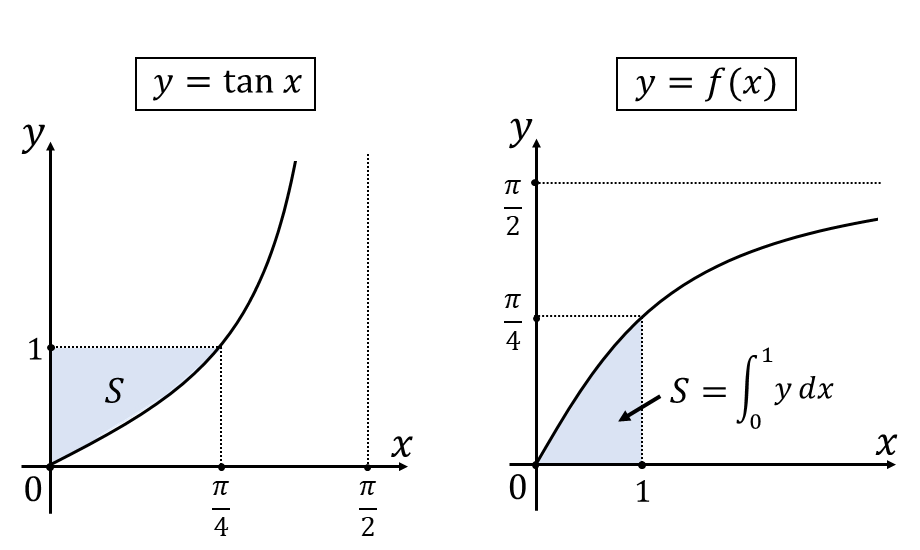
関数$\hspace{2pt}y=\tan x\hspace{2pt}$とその逆関数$\hspace{2pt}y=f(x)\hspace{2pt}$のグラフは、$\hspace{2pt}y=x\hspace{2pt}$に対して対称の関係となることから以下のようになります。 tanxの逆関数の定積分の問題

求める定積分$\displaystyle\hspace{2pt}\int_0^1 y\hspace{1pt}dx\hspace{2pt}$は、右側の青く塗られた部分の面積$\hspace{2pt}S\hspace{2pt}$となります。この面積が左側の青く塗られた部分と一致することを利用します。
　

【解答】
　問題 :『関数$\hspace{2pt}y=\tan x\hspace{2pt}$$\hspace{2pt}(\displaystyle \hspace{1pt} 0 \leqq x \leqq \frac{\pi}{4}\hspace{1pt})\hspace{2pt}$の逆関数を$\hspace{2pt}y=f(x)\hspace{2pt}$とする. このとき, $\displaystyle \int_0^1 f(x)\hspace{1pt}dx\hspace{2pt}$を求めよ.』
　

関数$\hspace{2pt}y=\tan x\hspace{2pt}$$\hspace{2pt}(\displaystyle \hspace{1pt} 0 \leqq x \leqq \frac{\pi}{4}\hspace{1pt})\hspace{2pt}$の逆関数を$\hspace{2pt}y=f(x)\hspace{2pt}$とすると $${\int_0^1 y\hspace{1pt}dx}$$ が求める定積分となります。

関数$\hspace{2pt}y=\tan x\hspace{2pt}$の逆関数は、$x = \tan y\hspace{2pt}$を$\hspace{2pt}y\hspace{2pt}$について解いた関数となります。

$\hspace{2pt}x = \tan y\hspace{2pt}$の両辺を$\hspace{2pt}y\hspace{2pt}$で微分すると $${\frac{dx}{dy} = \frac{1}{\cos^2 y}}$$ となります。

すなわち、$\displaystyle dx = \frac{1}{\cos^2 y}dy\hspace{2pt}$と表されます。

また、変数$\hspace{2pt}x\hspace{2pt}$の範囲に対応する変数$\hspace{2pt}y\hspace{2pt}$を求めると、以下のようになります。

${x}$	${0 \to 1}$
${y}$	$\displaystyle{0 \to \frac{\pi}{4}}$

よって、求める定積分は

$$ \begin{aligned} \hspace{10pt}& \int_0^1 f(x)\hspace{1pt}dx \\[1em] & = \int_0^1 y\hspace{1pt}dx \\[1em] & = \int_0^{\frac{\pi}{4}} y\cdot \frac{1}{\cos^2 y}dy \\[1em] & = \left[ y \tan y\right]_0^{\frac{\pi}{4}} - \int_0^{\frac{\pi}{4}} \tan y \hspace{1pt}dy \\[1em] & = \frac{\pi}{4} - \int_0^{\frac{\pi}{4}} \frac{\sin y}{\cos y} \hspace{1pt}dy \\[1em] & = \frac{\pi}{4} - [-\log |\cos y|]_0^{\frac{\pi}{4}} \\[1em] & = \frac{\pi}{4} + \log \frac{\sqrt{2}}{2} \\[1em] & = \frac{\pi}{4} - \frac{1}{2} \log 2 \\[1em] \end{aligned} $$

となります。

(上記の$\displaystyle\hspace{2pt}\int_0^{\frac{\pi}{4}} \frac{\sin y}{\cos y} \hspace{1pt}dy\hspace{2pt}$は被積分関数が $\displaystyle{\frac{f'(x)}{f(x)}}$ の形式であとき $${\int \frac{f'(x)}{f(x)}dx = \log |f(x)| + C}$$ となる関係を用いて計算しています。)
　

【別解】
　問題 :『関数$\hspace{2pt}y=\tan x\hspace{2pt}$$\hspace{2pt}(\displaystyle \hspace{1pt} 0 \leqq x \leqq \frac{\pi}{4}\hspace{1pt})\hspace{2pt}$の逆関数を$\hspace{2pt}y=f(x)\hspace{2pt}$とする。このとき、$\displaystyle \int_0^1 f(x)\hspace{1pt}dx\hspace{2pt}$を求めよ』
　

本問の定積分は、関数$\hspace{2pt}y=\tan x\hspace{2pt}$とその逆関数$\hspace{2pt}y=f(x)\hspace{2pt}$のグラフの関係性から求めることもできます。

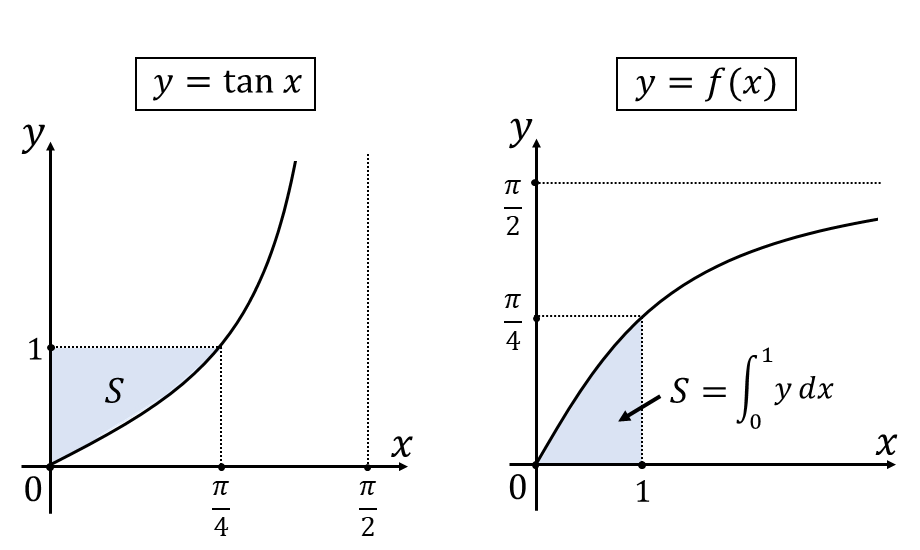
関数$\hspace{2pt}y=\tan x\hspace{2pt}$とその逆関数$\hspace{2pt}y=f(x)\hspace{2pt}$のグラフは、$\hspace{2pt}y=x\hspace{2pt}$に対して対称の関係となることから以下のように描くことができます。 tanxの逆関数の定積分の問題

ここで、求める定積分$\displaystyle\hspace{2pt}\int_0^1 f(x)\hspace{1pt}dx\hspace{2pt}$は上図の右側の青く塗られた部分の面積$\hspace{2pt}S\hspace{2pt}$となります。

この面積$\hspace{1pt}S\hspace{2pt}$は、上図の左側では関数$\hspace{2pt}y=\tan x\hspace{2pt}$、$y\hspace{1pt}$軸、$y=1\hspace{2pt}$に囲まれた面積に一致します。

よって、四角形の面積$\displaystyle\hspace{2pt}\frac{\pi}{4}\times 1\hspace{2pt}$から$\displaystyle\hspace{2pt}\int_0^{\frac{\pi}{4}}\tan x\hspace{1pt}dx\hspace{2pt}$により求められる面積を引けば、問題の定積分の値が求められます。

求める定積分の値は

$$ \begin{aligned} \hspace{10pt}& \int_0^1 f(x)\hspace{1pt}dx \\[1em] & = \frac{\pi}{4}\times 1 -\int_0^{\frac{\pi}{4}} \tan x\hspace{1pt}dx \\[1em] & = \frac{\pi}{4} - \int_0^{\frac{\pi}{4}} \frac{\sin x}{\cos x} \hspace{1pt}dx \\[1em] & = \frac{\pi}{4} - [-\log |\cos x|]_0^{\frac{\pi}{4}} \\[1em] & = \frac{\pi}{4} + \log \frac{\sqrt{2}}{2} \\[1em] & = \frac{\pi}{4} - \frac{1}{2} \log 2 \\[1em] \end{aligned} $$

と求められます。
　

\({x}\)	\({0 \to 1}\)
\({y}\)	\(\displaystyle{0 \to \frac{\pi}{4}}\)