円柱を切り取った部分の体積と断面積
◆第問目!
ただし、円柱の高さは\(\hspace{2pt}r \tan \theta\hspace{2pt}\)より高いとする。
(1) 立体の体積\(\hspace{1pt}V\hspace{1pt}\)を求めよ
(2) 切り口の断面積\(\hspace{1pt}S\hspace{1pt}\)を求めよ
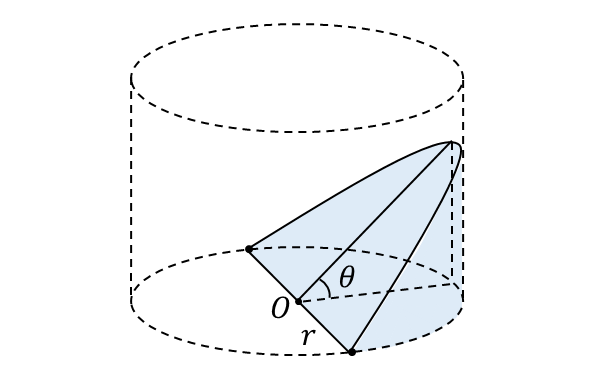
下図のように、円柱の直径上に\(\hspace{2pt}x\hspace{1pt}\)軸をとります。
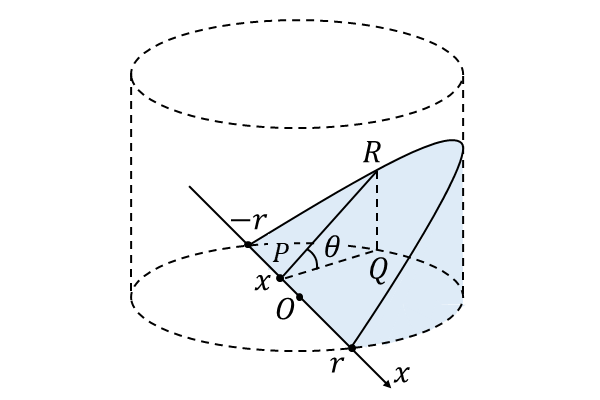
ここで、\(x\hspace{1pt}\)軸と垂直な平面で立体を切った断面の三角形\(\hspace{1pt}P\hspace{1pt}QR\hspace{1pt}\)の面積を\(\hspace{1pt}f(x)\hspace{1pt}\)とすると、求める立体の体積\(\hspace{1pt}V\hspace{1pt}\)は $${V = \int_{-r}^{r} f(x) dx}$$ と求められます。
ヒント(1)の図の三角形\(\hspace{1pt}P\hspace{1pt}QR\hspace{1pt}\)の斜辺\(\hspace{1pt}\overline{PR} \hspace{2pt}\)の長さを\(\hspace{1pt}g(x)\hspace{1pt}\)とすると、求める切り口の断面積\(\hspace{1pt}S\hspace{1pt}\)は $${S = \int_{-r}^{r} g(x) dx}$$ と求められます。
【答え】
(1) \(\displaystyle V = \frac{2}{3}r^3 \tan \theta\)
(2) \(\displaystyle S= \frac{\pi r^2}{2 \cos \theta}\)
【解答のポイント】
本問は断面積の積分から立体の体積を求める問題です。
以下の図のような曲線に囲まれた立体の体積\(\hspace{1pt}V\hspace{1pt}\)は、断面積が\(\hspace{1pt}S(x)\hspace{1pt}\)であるとき
$${V = \int_a^b S(x)\hspace{1pt}dx}$$
と求められます。
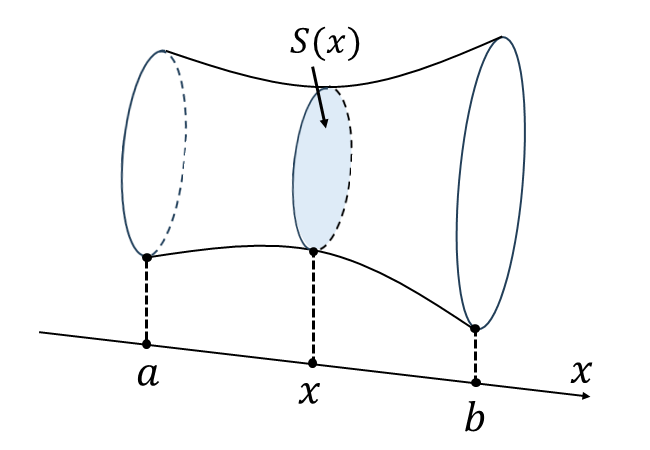
断面積を積分して体積を求める問題は、立体に対してどの向きを切った断面で積分するかがポイントになります。
本問では、以下の図のように円柱の直径上に\(\hspace{2pt}x\hspace{1pt}\)軸をとり、\(x\hspace{1pt}\)軸と垂直な平面で立体を切った断面を考えると、断面が三角形\(\hspace{1pt}P\hspace{1pt}QR\hspace{1pt}\)となり簡単に断面積を求めることができます。

【問題(1)の解答】
問題 :『底面が半径\(\hspace{1pt}r\hspace{1pt}\)の円柱を、底面の直径を含み底面と角度\(\hspace{1pt}\theta\hspace{1pt}\)をなす平面で切り取ったときの、平面より下側の立体について以下の問いに答えよ。
ただし、円柱の高さは\(\hspace{2pt}r \tan \theta\hspace{2pt}\)より高いとする。
(1) 立体の体積\(\hspace{1pt}V\hspace{1pt}\)を求めよ
(2) 切り口の断面積\(\hspace{1pt}S\hspace{1pt}\)を求めよ』
下図のように、円柱の直径上に\(\hspace{2pt}x\hspace{1pt}\)軸をとります。また、円柱の底面の中心が原点\(\hspace{1pt}O\hspace{1pt}\)に一致するとします。

\(x\hspace{1pt}\)軸と垂直な平面で立体を切った断面の三角形を\(\hspace{1pt}P\hspace{1pt}QR\hspace{1pt}\)とします。
このとき、辺\(\hspace{1pt}PQ\hspace{1pt}\)の長さは点\(\hspace{1pt}Q\hspace{1pt}\)が半径\(\hspace{1pt}r\hspace{1pt}\)の円上にあることから $${\overline{PQ} = \sqrt{r^2-x^2}}$$ となります。
また、辺\(\hspace{1pt}RQ\hspace{1pt}\)の長さは $$ \begin{aligned} \overline{RQ} &=\overline{PQ} \tan \theta \\[1em] &= \sqrt{r^2-x^2} \tan \theta\\[1em] \end{aligned} $$ となります。
すなわち、三角形\(\hspace{1pt}P\hspace{1pt}QR\hspace{1pt}\)の面積は
よって、求める立体の体積\(\hspace{1pt}V\hspace{1pt}\)は
と求められます。
【問題(2)の解答】
問題 :『底面が半径\(\hspace{1pt}r\hspace{1pt}\)の円柱を、底面の直径を含み底面と角度\(\hspace{1pt}\theta\hspace{1pt}\)をなす平面で切り取ったときの、平面より下側の立体について以下の問いに答えよ。
ただし、円柱の高さは\(\hspace{2pt}r \tan \theta\hspace{2pt}\)より高いとする。
(1) 立体の体積\(\hspace{1pt}V\hspace{1pt}\)を求めよ
(2) 切り口の断面積\(\hspace{1pt}S\hspace{1pt}\)を求めよ』
問題(1)と同様に、円柱の直径上に\(\hspace{2pt}x\hspace{1pt}\)軸をとります。また、円柱の底面の中心が原点\(\hspace{1pt}O\hspace{1pt}\)に一致するとします。
また、\(x\hspace{1pt}\)軸と垂直な平面で立体を切った断面の三角形を\(\hspace{1pt}P\hspace{1pt}QR\hspace{1pt}\)とします。

\(\overline{PQ} = \overline{PR} \cos \theta\hspace{2pt}\)であることから $$ \begin{aligned} \overline{PR} &= \frac{\overline{PQ}}{\cos \theta}\\[1em] &= \frac{ \sqrt{r^2-x^2}}{\cos \theta}\\[1em] \end{aligned} $$ となります。
すなわち、求める面積\(\hspace{1pt}S\hspace{1pt}\)は $$ \begin{aligned} S &= \int_{-r}^{r} \frac{ \sqrt{r^2-x^2}}{\cos \theta} \hspace{1pt}dx \\[1em] &= \frac{1}{\cos \theta}\int_{-r}^{r}\sqrt{r^2-x^2} \hspace{1pt}dx\\[1em] \end{aligned} $$ ここで、定積分\(\displaystyle \hspace{1pt} \int_{-r}^{r}\sqrt{r^2-x^2} \hspace{1pt}dx \hspace{2pt}\)は半径\(\hspace{1pt}r\hspace{1pt}\)の円の半分の面積となることから $${ \int_{-r}^{r}\sqrt{r^2-x^2} \hspace{1pt}dx = \frac{\pi r^2}{2}}$$ となります。
したがって
となります。
【入試本番に向けたアドバイス】
本問は、円柱を切り取った部分の体積と断面積を求めるです。
このような図形を切り取った部分の体積や断面積などを求める問題は、数学Ⅲの積分ではよく出題されるパターンの一つです。
類題としては『底面が楕円の柱体を切り取った部分』や『直線や放物線などの関数で囲まれた部分の回転体を切り取った部分』などの体積や断面積を求める問題があります。
本問はその中でも基本的な問題の一つであり、まずは本問の解答の流れを頭に入れておきましょう。
問題(2)の計算過程では、定積分\(\displaystyle\hspace{1pt}\int_{-r}^r \sqrt{r^2-x^2} \hspace{1pt} dx\hspace{1pt}\)が円の面積の半分であることから $${\int_{-r}^r \sqrt{r^2-x^2} \hspace{1pt} dx = \frac{\pi r^2}{2}}$$ とすることで定積分の計算を省略しました。
定積分の計算は、定積分を円や扇形、三角形など簡単な図形の面積と考えることで計算時間を大幅に減らすことができる場合があります。
『定積分を計算せずに済む方法はないか』を常に考えることが計算時間の短縮にとても重要となります。
【問題の種類を絞る】