水で満たされた半球を傾けたときの体積
◆第問目!
この半球を角度\(\hspace{1pt}\theta\hspace{1pt}\)だけ傾けたときに、初めに入っていた水と半球に残った水の体積比が\(\hspace{2pt}16 : 5\hspace{2pt}\)となるときの\(\hspace{2pt}\theta\hspace{1pt}\)を求めよ。(ただし、\(\displaystyle 0 < \theta < \frac{\pi}{2}\hspace{2pt}\)とする。)
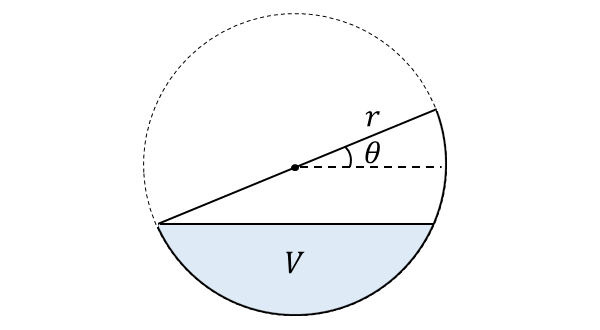
角度\(\hspace{1pt}\theta\hspace{1pt}\)だけ傾けたときに半球に残る水の体積は、半径\(\hspace{1pt}r\hspace{1pt}\)の球体から一部を切り取った部分の体積となります。
そこで、中心が原点となる円\(\hspace{2pt}x^2+y^2 = r^2\hspace{2pt}\)の回転体の体積から残った水の体積を求めます。
【答え】
\(\displaystyle \theta = \frac{\pi}{6}\)
【解答のポイント】
角度\(\hspace{1pt}\theta\hspace{1pt}\)だけ傾けたときに半球に残る水の体積は、半径\(\hspace{1pt}r\hspace{1pt}\)の球体から一部を切り取った部分の体積となります。
そこで、中心が原点となる円\(\hspace{2pt}x^2+y^2 = r^2\hspace{2pt}\)の回転体の体積から残った水の体積を求めます。
積分区間は、角度\(\hspace{1pt}\theta\hspace{1pt}\)と半径\(\hspace{1pt}r\hspace{1pt}\)から水の高さ方向の変化を式で表すことで定めることができます。
【解答】
問題 :『半径\(\hspace{1pt}r\hspace{1pt}\)の半球に水が満たされているとする。
この半球を角度\(\hspace{1pt}\theta\hspace{1pt}\)だけ傾けたときに、初めに入っていた水と半球に残った水の体積比が\(\hspace{2pt}16 : 5\hspace{2pt}\)となるときの\(\hspace{2pt}\theta\hspace{1pt}\)を求めよ。(ただし、\(\displaystyle 0 < \theta < \frac{\pi}{2}\hspace{2pt}\)とする。)』

下図のように、半球の断面図を時計回りに\(\hspace{2pt}90^\circ\hspace{2pt}\)だけ回転させて考えます。
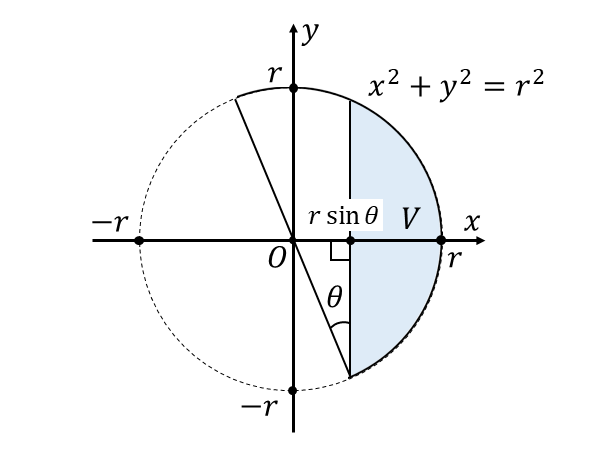
原点\(\hspace{2pt}O\hspace{2pt}\)に円の中心が一致しているとすると、上図の円の方程式は $${x^2 + y^2 = r^2}$$ となります。
半球に残った水の体積\(\hspace{1pt}V\hspace{2pt}\)は、上図の\(\hspace{1pt}x\hspace{1pt}\)の範囲\(\hspace{1pt}[r \sin \theta , r]\hspace{2pt}\)において\(\hspace{2pt}y=\sqrt{r^2 - x^2}\hspace{2pt}\)の回転体の体積を求めればよいので、以下のように求められます。
ここで、元の半球の容器に入っていた水の体積は $${\frac{1}{2}\cdot \frac{4}{3}\pi r^3 = \frac{2}{3}\pi r^3}$$ であることから $${V : \frac{2}{3}\pi r^3 = 5 : 16}$$ を解くと
ここで、\(f(x) = 8x^3 -24x + 11\hspace{2pt}\)とすると、因数定理から\(\hspace{2pt}f(\frac{1}{2}) = 0\hspace{2pt}\)となることから\(\hspace{2pt}f(x)\hspace{2pt}\)は\(\hspace{2pt}(x - \frac{1}{2})\hspace{2pt}\)を因数にもちます。
すなわち
となることから、\( 0 < \sin \theta < 1\hspace{2pt}\)を満たす解は\(\displaystyle\hspace{1pt} \sin \theta = \frac{1}{2}\hspace{2pt}\)となります。
したがって、求める\(\hspace{1pt}\theta\hspace{1pt}\)は\(\displaystyle\hspace{1pt}\theta = \frac{\pi}{6}\hspace{1pt}\)となります。
【入試本番に向けたアドバイス】
本問は、半球を傾けたときに残る水の体積の条件から半球の傾きを求める問題です。
水の入った容器を傾ける問題は、数学Ⅲの積分では頻出の問題パターンの一つです。
類題としては、『半球を傾けた角度の大きさから残った水の体積を求める問題』や『水の入った容器の形状が球体以外(放物線や対数関数などの回転体)の問題』などがあります。
本問はその中でも標準的な問題であるため、まずは本問の解答の流れを頭に入れておきましょう。
本問の計算過程で\(\hspace{2pt}8\sin^3 \theta -24\sin \theta + 11 = 0\hspace{2pt}\)を因数分解しました。
数学Ⅲの入試問題では当たり前のように三次方程式の因数分解が出てくるので、すぐに因数分解ができるように練習しておきましょう。
因数定理を用いるときに\(\hspace{2pt}f(\alpha)= 0\hspace{2pt}\)となる\(\hspace{2pt}\alpha\hspace{2pt}\)の候補は
\(\alpha = \hspace{2pt}\pm\)(定数項の約数)/(最高次の係数の約数)
から見つけます。
すなわち、\(8\sin^3 \theta -24\sin \theta + 11 = 0\hspace{2pt}\)となる\(\hspace{2pt}\sin \theta\hspace{2pt}\)の候補は $${\pm \frac{1}{1} , \pm \frac{1}{2} , \pm \frac{1}{4} , \pm \frac{1}{8} , }$$ $${\pm \frac{11}{1} , \pm \frac{11}{2} , \pm \frac{11}{4} , \pm \frac{11}{8}}$$ に限られます。
候補となる数は多いですが、最終的に\(\displaystyle\hspace{1pt}0 < \theta < \frac{\pi}{2}\hspace{2pt}\)の範囲で\(\hspace{1pt}\theta\hspace{1pt}\)を求めることから\(\displaystyle \hspace{2pt} \frac{1}{2} \hspace{1pt},\hspace{1pt} \frac{1}{4} \hspace{1pt},\hspace{1pt} \frac{1}{8}\hspace{2pt}\)あたりだと目星をつけてチェックしていきましょう。
【問題の種類を絞る】