-光と光学に関連する用語の解説サイト-

楕円の回転体の体積

◆第問目！

【 数Ⅲ : 難易度 ★ 】
　\(\displaystyle{\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\hspace{2pt}}\)\({(\hspace{1pt}a,b>0\hspace{2pt}\hspace{1pt})}\) に囲まれた部分を\({\hspace{1pt}x}\)軸の周りに回転させた回転体の体積を求めよ

楕円の回転体の体積を求める問題です。

区間\({\hspace{1pt}[a,b]\hspace{2pt}}\)において関数\({\hspace{1pt}f(x)\hspace{2pt}}\)と\({\hspace{1pt}x=a,x=b\hspace{2pt}}\)によって囲まれる部分を\({\hspace{1pt}x\hspace{2pt}}\)軸の周りに回転させた回転体の体積\(\hspace{1pt}V\hspace{1pt}\)は

$$\hspace{10pt}{V= \pi \int_a^b (f(x))^2 \hspace{1pt}dx }\hspace{10pt}$$

と求められます。

【答え】
　\(\displaystyle \frac{4}{3} \pi a b^2 \)
　

【解答のポイント】
本問は楕円の回転体の体積を求める問題です。

区間\({\hspace{1pt}[a,b]\hspace{2pt}}\)において関数\({\hspace{1pt}f(x)\hspace{2pt}}\)と\({\hspace{1pt}x=a,x=b\hspace{2pt}}\)によって囲まれる部分を\({\hspace{1pt}x\hspace{2pt}}\)軸の周りに回転させた回転体の体積は

$$\hspace{10pt}{V= \pi \int_a^b (f(x))^2 \hspace{1pt}dx }\hspace{10pt}$$

と求められます。

【解答】
　問題 : 『 \(\displaystyle{\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\hspace{2pt}}\)\({(\hspace{1pt}a,b>0\hspace{2pt}\hspace{1pt})}\) に囲まれた部分を\({\hspace{1pt}x}\)軸の周りに回転させた回転体の体積を求めよ』
　

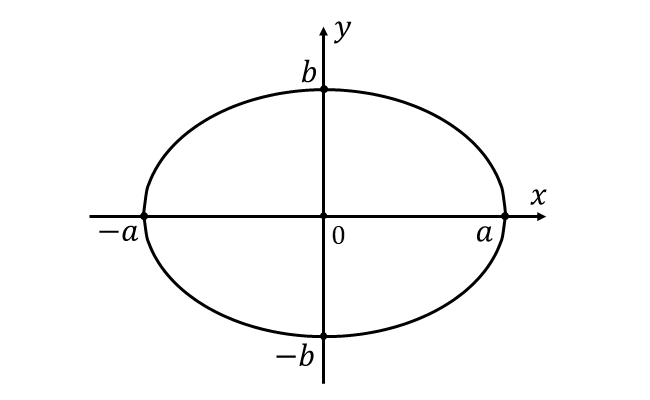
問題の楕円を図に描くと以下のようになります。 楕円の回転体の体積を求める問題

上図から、楕円を\({\hspace{1pt}x}\)軸の周りに回転させた回転体の体積は以下のように求められます。

$$ \begin{aligned} \hspace{10pt}& \pi \int_{-a}^{a} y^2 \hspace{1pt}dx \\[1em] & = 2 \pi \int_{0}^{a} \left(b^2 - \frac{b^2}{a^2}x^2 \right) \hspace{1pt}dx\\[1em] & = 2 \pi b^2\left[x - \frac{1}{3a^2}x^3 \right]_{0}^{a} \\[1em] & = 2 \pi b^2 \left(a - \frac{1}{3a^2} \times a^3 \right) \\[1em] & = 2 \pi b^2 \left(a - \frac{a}{3} \right) \\[1em] & = \frac{4}{3} \pi a b^2 \\[1em] \end{aligned} $$

と求められます。

【出題範囲】　　【難易度】



　




　【問題の種類を絞る】



Copyright (c) 光学技術の基礎用語 All Rights Reserved.