-光と光学に関連する用語の解説サイト-

y=sinxとy=cosxに囲まれた部分の回転体の体積

◆第問目！

【 数Ⅲ : 難易度 ★★★ 】
　\({y=\sin x\hspace{2pt},}\)\({\hspace{3pt}y= \cos x\hspace{2pt}}\)\({\left(\frac{\pi}{4} \leqq x \leqq \frac{5}{4}\pi\hspace{1pt}\right)}\) に囲まれた部分を\({\hspace{1pt}x}\)軸の周りに回転させた回転体の体積を求めよ

\({y=\sin x\hspace{2pt},}\)\({\hspace{3pt}y= \cos x\hspace{2pt}}\)のグラフを描くと、回転する部分が\({x\hspace{1pt}}\)軸をまたいでいることが分かります。

\({x\hspace{1pt}}\)軸をまたいでいる部分の回転体の体積を求めるときは、\({\hspace{2pt}y< 0 \hspace{2pt}}\)となる箇所を\({\hspace{1pt}x\hspace{2pt}}\)軸で折り返したグラフを描くと分かりやすくなります。

【答え】
　\(\displaystyle \frac{(\pi + 6)\pi}{4} \)
　

【解答のポイント】
\({y=\sin x\hspace{2pt},}\)\({\hspace{3pt}y= \cos x\hspace{2pt}}\)のグラフを描くと、回転する部分が\({x\hspace{1pt}}\)軸をまたいでいることが分かります。

\({x\hspace{1pt}}\)軸をまたいでいる部分の回転体の体積を求めるときは、\({\hspace{1pt}y< 0 \hspace{2pt}}\)となる箇所を\({\hspace{1pt}x\hspace{2pt}}\)軸で折り返した部分を含めて回転体を考えます。

区間\({\hspace{1pt}[a,b]\hspace{2pt}}\)において関数\({\hspace{1pt}f(x) \geqq g(x) \geqq 0 \hspace{2pt}}\)であるとき、この2つの曲線と\({\hspace{1pt}x=a,x=b\hspace{2pt}}\)によって囲まれる部分を\({\hspace{1pt}x\hspace{2pt}}\)軸の周りに回転させた回転体の体積\(\hspace{1pt}V\hspace{1pt}\)は

$$\hspace{10pt}{V= \pi \int_a^b (f(x))^2 \hspace{1pt}dx - \pi \int_a^b (g(x))^2 \hspace{1pt}dx}\hspace{10pt}$$

と求められます。
　

【解答】
　問題 : 『 \({y=\sin x\hspace{2pt},}\)\({\hspace{3pt}y= \cos x\hspace{2pt}}\)\({\left(\frac{\pi}{4} \leqq x \leqq \frac{5}{4}\pi\hspace{1pt}\right)}\) に囲まれた部分を\({\hspace{1pt}x}\)軸の周りに回転させた回転体の体積を求めよ』
　

まず、\({y=\sin x\hspace{2pt},}\)\({\hspace{3pt}y= \cos x\hspace{2pt}}\)の交点の座標は $${x = \frac{\pi}{4}\hspace{1pt},\hspace{1pt}\frac{5}{4}\pi}$$ となります。

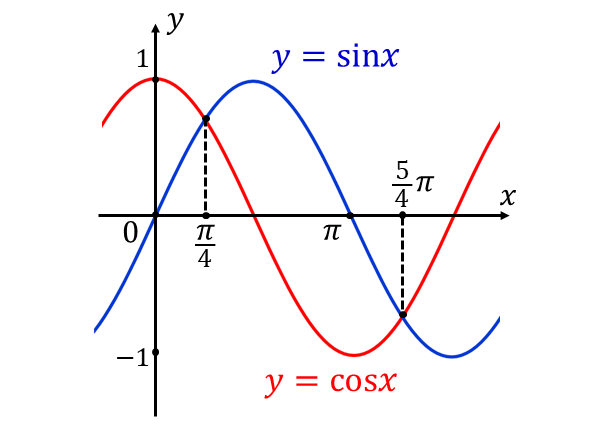
\({y=\sin x\hspace{2pt},}\)\({\hspace{3pt}y= \cos x\hspace{2pt}}\)のグラフを描くと以下のようになります。 y=sinx,y=cosxに囲まれた部分の図

ここで、上図から\({\hspace{1pt}y=\sin x\hspace{2pt},}\)\({\hspace{3pt}y= \cos x\hspace{2pt}}\)は\({\hspace{1pt}x\hspace{2pt}}\)軸をまたいでいるため、\({\hspace{1pt}y< 0 \hspace{2pt}}\)となる箇所を\({\hspace{1pt}x\hspace{2pt}}\)軸で折り返した部分を含めて回転体を考えます。

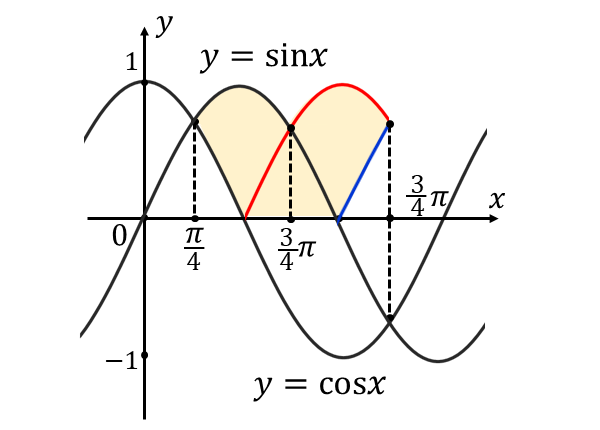
以下に、\({\hspace{1pt}y< 0 \hspace{2pt}}\)となる箇所を\({\hspace{1pt}x\hspace{1pt}}\)軸で折り返した部分を含めた図を示します。図中の黄色に塗られた部分が回転すると考えて積分します。 y=sinx,y=cosxに囲まれた部分のうち、x軸をまたぐ部分を折り返した図

上図から、回転する部分は\(\displaystyle{\hspace{1pt}x=\frac{3}{4}\pi\hspace{2pt}}\)で対称となっていることが分かります。

そのため、区間\(\displaystyle \hspace{1pt}\left[\frac{\pi}{4},\frac{3}{4}\pi \right]\hspace{1pt}\)で求められる体積を2倍して全体の体積を求めます。

以上から、回転体の体積は以下のように求められます。

$$ \begin{aligned} \hspace{10pt}& 2 \left( \pi \int_{\frac{\pi}{4}}^{\frac{3}{4}\pi} \sin^2 x \hspace{1pt}dx - \pi \int_{\frac{\pi}{4}}^{\frac{\pi}{2}} \cos^2 x \hspace{1pt}dx \right) \\[1.3em] & = 2 \pi \left(\int_{\frac{\pi}{4}}^{\frac{3}{4}\pi} \frac{1-\cos 2x}{2} \hspace{1pt}dx - \int_{\frac{\pi}{4}}^{\frac{\pi}{2}} \frac{1+\cos 2x}{2} \hspace{1pt}dx \right) \\[1.3em] & = \pi \left(\int_{\frac{\pi}{4}}^{\frac{3}{4}\pi} (1-\cos 2x)\hspace{1pt}dx - \int_{\frac{\pi}{4}}^{\frac{\pi}{2}}(1+\cos 2x)\hspace{1pt}dx \right) \\[1.3em] & = \pi \left (\left[ x -\frac{1}{2}\sin 2x \right]_{\frac{\pi}{4}}^{\frac{3}{4}\pi} -\left[ x +\frac{1}{2}\sin 2x \right]_{\frac{\pi}{4}}^{\frac{\pi}{2}} \right)\\[1.3em] & = \pi \left (\frac{3}{4}\pi - \frac{\pi}{4} -\frac{1}{2}(-1-1) - \left(\frac{\pi}{2} - \frac{\pi}{4}\right) -\frac{1}{2}(0-1)\right)\hspace{10pt}\\[1.3em] & = \pi \left (\frac{1}{4}\pi +\frac{3}{2}\right)\\[1.3em] & =\frac{(\pi + 6)\pi}{4}\\[1.3em] \end{aligned} $$

と求められます。

(上記の計算過程には半角の公式 $$\displaystyle{\sin^2 x = \frac{1-\cos 2x}{2}}$$ $$\displaystyle{\cos^2 x = \frac{1+\cos 2x}{2}}$$を使用しています。)
　

【入試本番に向けたアドバイス】
　①回転する部分と回転軸の関係を明確にする
　本問は、三角関数\({\hspace{1pt}y=\sin x\hspace{2pt},}\)\({\hspace{3pt}y= \cos x\hspace{2pt}}\)に囲まれた部分の回転体の体積を求める問題です。

本問のように、\(x\hspace{1pt}\)軸のまわりを回転する回転体において、\(x\hspace{1pt}\)軸をまたいだ部分のある場合は、\(\hspace{2pt}y < 0 \hspace{2pt}\)の部分を\(\hspace{1pt}x\hspace{1pt}\)軸で折り返して考える点に注意が必要です。

そのため、回転体の問題では必ずグラフを描き、回転する部分と回転軸との関係を明確にしておきましょう。
　

　

②三角関数の積分は対称性を利用する
　三角関数は周期性をもつ関数のため、三角関数を含む積分では対称性を利用して計算量を少なくできることが多いです。

本問の解答でも、対称性を利用して区間\(\displaystyle\hspace{1pt}\left[\frac{\pi}{4} , \frac{5}{4}\pi \right]\hspace{1pt}\)の回転体の体積を、区間\(\displaystyle\hspace{1pt}\left[\frac{\pi}{4} , \frac{3}{4}\pi \right]\hspace{1pt}\)の体積を二倍することで求めています。
　

【出題範囲】　　【難易度】



　




　【問題の種類を絞る】



Copyright (c) 光学技術の基礎用語 All Rights Reserved.