ユークリッドの互除法
本項では以下の内容を解説しています。
- ・ユーグリッドの互除法とは
- ・ユークリッドの互除法の証明
- ・問題と解き方
1. ユークリッドの互除法
ユークリッドの互除法とは、\(2\hspace{1pt}\)つの整数の最大公約数を効率よく求めるための手法です。
まず、最大公約数について説明した後、ユークリッドの互除法について解説します。
1-1. 最大公約数とは
最大公約数とは、\({2\hspace{2pt}}\)つ以上の整数に共通する約数の中で最も大きい約数のことをいいます。
例えば、\({12\hspace{2pt}}\)と\({\hspace{1pt}18\hspace{2pt}}\)の最大公約数を調べると
\({12\hspace{2pt}}\)の正の約数が $${\color{black}{}1\hspace{2pt},\hspace{2pt}2\hspace{2pt},\hspace{2pt}3\hspace{2pt},\hspace{2pt}4\hspace{2pt},\hspace{2pt}\color{red}{}6\color{black}{}\hspace{2pt},\hspace{2pt}12}$$ \({18\hspace{2pt}}\)の正の約数が $${\color{black}{}1\hspace{2pt},\hspace{2pt}2\hspace{2pt},\hspace{2pt}3\hspace{2pt},\hspace{2pt}\color{red}{}6\color{black}{}\hspace{2pt},\hspace{2pt}18}$$ であり、\({12\hspace{2pt}}\)と\({\hspace{1pt}18\hspace{2pt}}\)に共通する約数は $${\color{black}{}1\hspace{2pt},\hspace{2pt}2\hspace{2pt},\hspace{2pt}3\hspace{2pt},\hspace{2pt}\color{red}{}6}$$ となります。すなわち、最大公約数は\({\hspace{1pt}6\hspace{2pt}}\)となります。
ある整数の組の最大公約数を求めるには
① それぞれの整数の約数を調べる
② 共通する約数を探す
③ ②の中で最大の数を選ぶ
という手順を踏む必要があります。
上記の\({\hspace{2pt}12\hspace{2pt}}\)と\({\hspace{1pt}18\hspace{2pt}}\)のように小さい整数の組では、それぞれの約数をすぐに求められるため、最大公約数を簡単に求めることができます。
一方、\(123246\hspace{2pt}\)と\(\hspace{1pt}547230\hspace{2pt}\)のように大きい整数の組では、『①約数を探す』の段階で多くの計算が必要となり、最大公約数を求めることが難しくなります。
1-2. ユークリッドの互除法とは
ユークリッドの互除法とは、大きい整数の組の最大公約数を効率よく求めることができる手法です。
\(2\hspace{2pt}\)つの数\(\hspace{1pt}a\hspace{1pt},\hspace{1pt}b\hspace{1pt}\)\(\hspace{1pt}(a > b)\hspace{2pt}\)に対して、以下の方法で最大公約数を求めることができます。
① \(a\hspace{2pt}\)を\(\hspace{1pt}b\hspace{2pt}\)で割り、余り\(\hspace{1pt}r_1\hspace{2pt}\)を求める
② \(b\hspace{2pt}\)を\(\hspace{1pt}r_1\hspace{2pt}\)で割り、余り\(\hspace{1pt}r_2\hspace{2pt}\)を求める
③ \(r_1\hspace{2pt}\)を\(\hspace{1pt}r_2\hspace{2pt}\)で割り、余り\(\hspace{1pt}r_3\hspace{2pt}\)を求める
\(\hspace{1pt}\cdots \cdots\hspace{2pt}\)
この操作を余りが\(\hspace{1pt}0\hspace{2pt}\)になるまで繰り返したとき
最後に割った数が最大公約数となる
1-3. ユークリッドの互除法の計算例
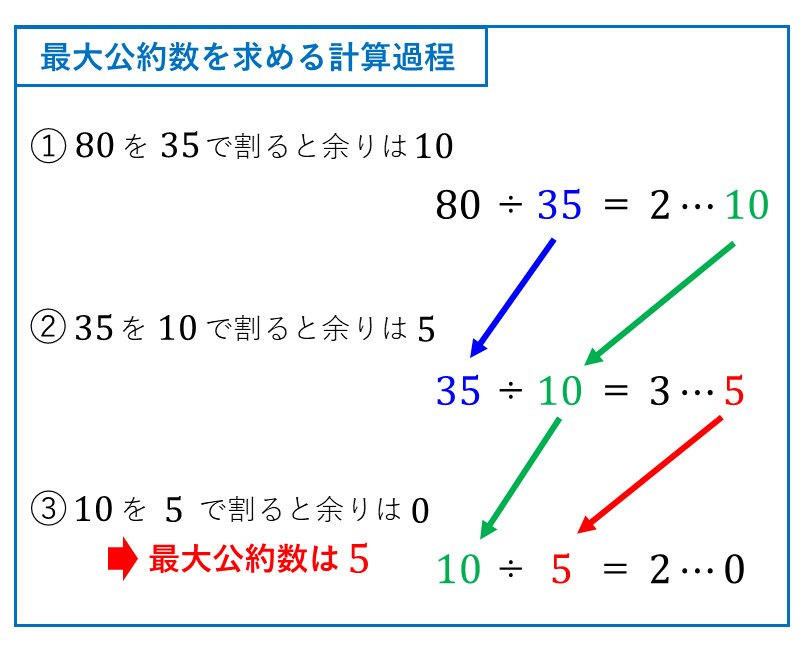
計算例として、ユークリッドの互除法から\(\hspace{2pt}80\hspace{2pt}\)と\(\hspace{1pt}35\hspace{2pt}\)の最大公約数を求める過程を示します。
以下のように、①~③の計算をすることで最大公約数は\(\hspace{1pt}5\hspace{1pt}\)と求めることができます。
2. ユークリッドの互除法の証明
ユークリッドの互除法は、整数の割り算に関して以下の性質が成り立つことを利用しています。
『\(\hspace{1pt}a\hspace{2pt}\)と\(\hspace{1pt}b\hspace{2pt}\)の最大公約数』と『\(\hspace{1pt}b\hspace{2pt}\)と\(\hspace{1pt}r\hspace{2pt}\)の最大公約数』が等しい
上記の割り算の性質を証明することで、ユーグリッドの互除法が成り立つことを示します。
整数\(\hspace{1pt}a\hspace{1pt},\hspace{1pt}b\hspace{2pt}(a \geqq b)\hspace{2pt}\)に対して以下の式が成り立つとします。 $${a = b\hspace{1pt}q + r}$$ (上式は\(\hspace{1pt}a\hspace{2pt}\)を\(\hspace{1pt}b\hspace{2pt}\)で割ったときの商が\(\hspace{1pt}q\hspace{1pt},\hspace{2pt}\)余りが\(\hspace{1pt}r\hspace{2pt}\)であることを意味しています。)
ここで
\(a\hspace{1pt},\hspace{1pt}b\hspace{2pt}\)の最大公約数を\(\hspace{1pt}g\hspace{1pt}c\hspace{1pt}d\hspace{1pt}(a\hspace{1pt},\hspace{1pt}b)\hspace{1pt}\)
\(b\hspace{1pt},\hspace{1pt}r\hspace{2pt}\)の最大公約数を\(\hspace{1pt}g\hspace{1pt}c\hspace{1pt}d\hspace{1pt}(b\hspace{1pt},\hspace{1pt}r)\hspace{1pt}\)
とします。
(\(\hspace{1pt}g\hspace{1pt}c\hspace{1pt}d\hspace{2pt}\)は最大公約数を表す Greatest Common Divisor の略です。)
【(1)\(\hspace{1pt}g\hspace{1pt}c\hspace{1pt}d\hspace{1pt}(b\hspace{1pt},\hspace{1pt}r) \leqq g\hspace{1pt}c\hspace{1pt}d\hspace{1pt}(a\hspace{1pt},\hspace{1pt}b)\hspace{1pt}\)の証明】
\(\hspace{1pt}g\hspace{1pt}c\hspace{1pt}d\hspace{1pt}(b\hspace{1pt},\hspace{1pt}r)\hspace{1pt}\)は、\(b\hspace{2pt}\)と\(\hspace{1pt}r\hspace{2pt}\)のどちらも割り切れる数です。そのため、以下の式
$${a = b\hspace{1pt}q + r}$$
の右辺全体も\(\hspace{1pt}g\hspace{1pt}c\hspace{1pt}d\hspace{1pt}(b\hspace{1pt},\hspace{1pt}r)\hspace{1pt}\)で割り切れます。つまり\(\hspace{2pt}a\hspace{2pt}\)も\(\hspace{1pt}g\hspace{1pt}c\hspace{1pt}d\hspace{1pt}(b\hspace{1pt},\hspace{1pt}r)\hspace{1pt}\)で割り切れます。
(\(\hspace{1pt}b=m \times g\hspace{1pt}c\hspace{1pt}d\hspace{1pt}(b\hspace{1pt},\hspace{1pt}r)\hspace{1pt},r=n \times g\hspace{1pt}c\hspace{1pt}d\hspace{1pt}(b\hspace{1pt},\hspace{1pt}r)\hspace{2pt}\)を満たす整数\(\hspace{1pt}m\hspace{1pt},\hspace{1pt}n\hspace{2pt}\)が存在することから\(\hspace{2pt}a = b\hspace{1pt}q+r = g\hspace{1pt}c\hspace{1pt}d\hspace{1pt}(b\hspace{1pt},\hspace{1pt}r)(m\hspace{1pt}q+n)\hspace{2pt}\)より、\(a\hspace{2pt}\)は\(\hspace{1pt}g\hspace{1pt}c\hspace{1pt}d\hspace{1pt}(b\hspace{1pt},\hspace{1pt}r)\hspace{2pt}\)で割り切れます。)
よって\(\hspace{2pt}g\hspace{1pt}c\hspace{1pt}d\hspace{1pt}(b\hspace{1pt},\hspace{1pt}r)\hspace{1pt}\)は\(\hspace{2pt}a\hspace{2pt}\)も\(\hspace{2pt}b\hspace{2pt}\)も割り切れる数(公約数)となります。
\(a\hspace{2pt}\)と\(\hspace{1pt}b\hspace{2pt}\)の最大公約数は\(\hspace{1pt}g\hspace{1pt}c\hspace{1pt}d\hspace{1pt}(a\hspace{1pt},\hspace{1pt}b)\hspace{2pt}\)であるから
$${g\hspace{1pt}c\hspace{1pt}d\hspace{1pt}(b\hspace{1pt},\hspace{1pt}r) \leqq g\hspace{1pt}c\hspace{1pt}d\hspace{1pt}(a\hspace{1pt},\hspace{1pt}b)}$$
が成り立ちます。
【(2)\(\hspace{1pt}g\hspace{1pt}c\hspace{1pt}d\hspace{1pt}(a\hspace{1pt},\hspace{1pt}b) \leqq g\hspace{1pt}c\hspace{1pt}d\hspace{1pt}(b\hspace{1pt},\hspace{1pt}r)\hspace{1pt}\)の証明】 $${a = b\hspace{1pt}q + r}$$ を変形すると $${r = a- b\hspace{1pt}q }$$ となります。
\(\hspace{1pt}g\hspace{1pt}c\hspace{1pt}d\hspace{1pt}(a\hspace{1pt},\hspace{1pt}b)\hspace{1pt}\)は\(\hspace{1pt}a\hspace{2pt}\)と\(\hspace{1pt}b\hspace{2pt}\)のどちらも割り切れる数です。そのため、以下の式 $${r = a- b\hspace{1pt}q}$$ の右辺全体も\(\hspace{1pt}g\hspace{1pt}c\hspace{1pt}d\hspace{1pt}(a\hspace{1pt},\hspace{1pt}b)\hspace{1pt}\)で割り切れます。つまり\(\hspace{2pt}r\hspace{2pt}\)も\(\hspace{1pt}g\hspace{1pt}c\hspace{1pt}d\hspace{1pt}(a\hspace{1pt},\hspace{1pt}b)\hspace{1pt}\)で割り切れます。
(\(\hspace{1pt}a=m \times g\hspace{1pt}c\hspace{1pt}d\hspace{1pt}(a\hspace{1pt},\hspace{1pt}b)\hspace{1pt},b=n \times g\hspace{1pt}c\hspace{1pt}d\hspace{1pt}(a\hspace{1pt},\hspace{1pt}b)\hspace{2pt}\)を満たす整数\(\hspace{1pt}m\hspace{1pt},\hspace{1pt}n\hspace{2pt}\)が存在することから\(\hspace{2pt}r = a-b\hspace{1pt}q = g\hspace{1pt}c\hspace{1pt}d\hspace{1pt}(a\hspace{1pt},\hspace{1pt}b)(m-n\hspace{1pt}q)\hspace{2pt}\)より、\(r\hspace{2pt}\)は\(\hspace{1pt}g\hspace{1pt}c\hspace{1pt}d\hspace{1pt}(a\hspace{1pt},\hspace{1pt}b)\hspace{2pt}\)で割り切れます。)
よって\(\hspace{2pt}g\hspace{1pt}c\hspace{1pt}d\hspace{1pt}(a\hspace{1pt},\hspace{1pt}b)\hspace{1pt}\)は\(\hspace{2pt}b\hspace{2pt}\)も\(\hspace{2pt}r\hspace{2pt}\)も割り切れる数(公約数)となります。
\(b\hspace{2pt}\)と\(\hspace{1pt}r\hspace{2pt}\)の最大公約数は\(\hspace{1pt}g\hspace{1pt}c\hspace{1pt}d\hspace{1pt}(b\hspace{1pt},\hspace{1pt}r)\hspace{2pt}\)であるから
$${g\hspace{1pt}c\hspace{1pt}d\hspace{1pt}(a\hspace{1pt},\hspace{1pt}b) \leqq g\hspace{1pt}c\hspace{1pt}d\hspace{1pt}(b\hspace{1pt},\hspace{1pt}r)}$$
が成り立ちます。
(1)式
$${g\hspace{1pt}c\hspace{1pt}d\hspace{1pt}(b\hspace{1pt},\hspace{1pt}r) \leqq g\hspace{1pt}c\hspace{1pt}d\hspace{1pt}(a\hspace{1pt},\hspace{1pt}b)}$$
と(2)式
$${g\hspace{1pt}c\hspace{1pt}d\hspace{1pt}(a\hspace{1pt},\hspace{1pt}b) \leqq g\hspace{1pt}c\hspace{1pt}d\hspace{1pt}(b\hspace{1pt},\hspace{1pt}r)}$$
がともに成り立つことから
$${g\hspace{1pt}c\hspace{1pt}d\hspace{1pt}(a\hspace{1pt},\hspace{1pt}b) = g\hspace{1pt}c\hspace{1pt}d\hspace{1pt}(b\hspace{1pt},\hspace{1pt}r)}$$
が示されます。(\(\hspace{1pt}m \geqq n\hspace{2pt}\)かつ\(\hspace{1pt}m \leqq n\hspace{2pt}\)が成り立つのは\(\hspace{1pt}m=n\hspace{2pt}\)のときのみという関係を用いています。)
以上から $${a = b\hspace{1pt}q + r}$$ における『\(\hspace{1pt}a\hspace{2pt}\)と\(\hspace{1pt}b\hspace{2pt}\)の最大公約数』と『\(\hspace{1pt}b\hspace{2pt}\)と\(\hspace{1pt}r\hspace{2pt}\)の最大公約数』が一致します。
余り\(\hspace{1pt}r\hspace{2pt}\)は割る数\(\hspace{1pt}b\hspace{2pt}\)よりも小さくなるため、整数の割り算を繰り返し行うと有限の回数で余りが\(\hspace{1pt}0\hspace{2pt}\)となります。
ここで、\(0\hspace{2pt}\)はどの整数でも割り切れるため、ある整数\(\hspace{1pt}b\hspace{2pt}\)と\(\hspace{1pt}0\hspace{2pt}\)の最大公約数は\(\hspace{1pt}b\hspace{2pt}\)となります。
したがって、ユーグリッドの互除法により最大公約数が求められることが証明されます。
3. ユーグリッドの互除法の問題
本章では、ユーグリッドの互除法に関連する問題と解き方について解説します。
【答え】
最大公約数は\(\hspace{1pt}12 \hspace{2pt}\)
【解答】
最大公約数をユークリッドの互除法から求めます。
まず、\(420\hspace{2pt}\)を\(\hspace{1pt}288\hspace{2pt}\)で割ると $${420 \div 288 = 1 \cdots 132}$$ 次に、\(288\hspace{2pt}\)を\(\hspace{1pt}132\hspace{2pt}\)で割ると $${288 \div 132 = 2 \cdots 24}$$ 次に、\(132\hspace{2pt}\)を\(\hspace{1pt}24\hspace{2pt}\)で割ると $${132 \div 24 = 5 \cdots 12}$$ 次に、\(24\hspace{2pt}\)を\(\hspace{1pt}12\hspace{2pt}\)で割ると $${24 \div 12 = 2 \cdots 0}$$ から余りが\(\hspace{1pt}0\hspace{2pt}\)となることから、最大公約数は\(\hspace{1pt}12\hspace{2pt}\)となります。
\(\displaystyle{\frac{14175}{11907}}\)
【答え】
\(\displaystyle\hspace{1pt}\frac{25}{21}\hspace{2pt}\)
【解答のポイント】
分数を約分するためには、分母と分子の数の最大公約数を見つけて割る必要があります。
通常は分母と分子の数をそれぞれ素因数分解をして最大公約数を見つけますが、大きい数であるため最大公約数を見つけるために計算に時間がかかります。
(この最大公約数の解説記事の問題(3)では、同じ分数を実際に素因数分解から計算しています。)
そこで、分母と分子の数にユーグリッドの互除法を適用し、最大公約数を見つけて約分します。
【解答】
分子の\(\hspace{1pt}14175\hspace{2pt}\)と分母の\(\hspace{1pt}11907\hspace{2pt}\)の最大公約数をユークリッドの互除法から求めます。
まず、\(14175\hspace{2pt}\)を\(\hspace{1pt}11907\hspace{2pt}\)で割ると $${14175 \div 11907 = 1 \cdots 2268}$$ 次に、\(11907\hspace{2pt}\)を\(\hspace{1pt}2268\hspace{2pt}\)で割ると $${11907 \div 2268 = 5 \cdots 567}$$ 次に、\(2268\hspace{2pt}\)を\(\hspace{1pt}567\hspace{2pt}\)で割ると $${2268 \div 567 = 4 \cdots 0}$$ から余りが\(\hspace{1pt}0\hspace{2pt}\)となることから、最大公約数は\(\hspace{1pt}567\hspace{2pt}\)となります。
したがって、求める約分の結果は分子と分母を\({\hspace{1pt}567\hspace{2pt}}\)で割ればよいので $${\frac{14175}{11907} =\frac{14175 \div 567}{11907 \div 567}= \frac{25}{21}}$$ と求められます。